树：R树

空间数据

基于实体的模型：

1. 0-dimensional objects：一般使用点point来表示那些对于不需要使用到形状信息的实体。
2. 1-dimensional objects or linear objects：用于表示一些路网的边，一般用于表示道路road。 (polyline)
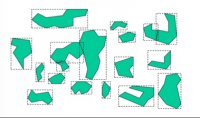
3. 2-dimensional objects or surfacic objects：用于表示有区域面积的实体。 (polygon)

常用的空间数据查询方式：

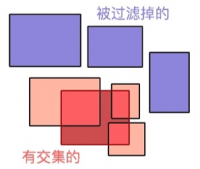
1. 窗口查询：给定一个查询窗口（通常是一个矩形），返回与查询窗口相重叠的物体。
2. 点查询：给定一个点，返回包含这个点的所有几何图形。

空间数据获取的方法

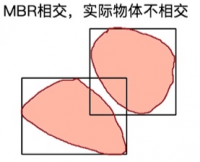
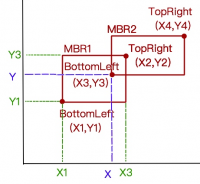
通常，我们不选择去索引几何物体本身，而是采用“最小限定箱”（MBB：minimum bounding box）作为不规则几何图形的 key 来构建空间索引：

1. 二维：称之为“最小限定矩形”（MBR：minimum bounding retangle）。

   

2. 三维：称之为“最小限定箱”（MBB：minimum bounding box）。

   

通过索引操作对象的 MBB 进行查询，步骤：【？？？】

1. Filtering：过滤掉 MBB 不相交的数据集，剩下的 MBB 被索引到的称为一个数据的超集。

   

2. Refinement：测试实际的几何形状会不会满足查询条件，精确化。

   

使用：

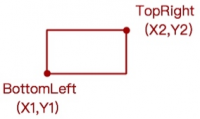
1. 用数据表示一个 MBR：

   通常，只需要两个点就可限定一个矩形，也就是矩形某个对角线的两个点（“左下右上”或“左上右下”）就可以决定一个唯一的矩形。

   

   1. 表示一个点的数据：

   　　　　public class Point{ //用一个类来表示一个点
   　　　　    public Float x;
   　　　　    public Float y
   　　　　}
   

   1. 表示一个 MBR 的数据：

   　　　　public class MBR{
   　　　　    public Point BottomLeft;
   　　　　    public Point TopRight;
   　　　　}
   

2. 判断两个 MBR 是否相交：

   如果一个MBR的TopLeft或者BottomRight的（x，y）位于另一个MBR的 xRange 和 yRangle 里面，则说明这两个MBR相交。

   

---

---

---

参考

1. 什么是R树？
2. 空间数据索引RTree（R树）完全解析及Java实现
3. 从B树、B+树、B*树谈到R 树
4. []
5. []