树：B+树

关于

B+树 是 B树 的一种变形形式，也是一种多路搜索树，但查询性能更好。

• B+树（B+-tree）操作模拟：https://www.cs.usfca.edu/~galles/visualization/BPlusTree.html

定义、结构、特点

B+树 特点是：能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。

定义

基础定义与 B树 基本等价（包括关键字及子树的个数要求等）。

不同点：“关键字个数”与“子节点个数（子树个数）”，有两种不同的定义：

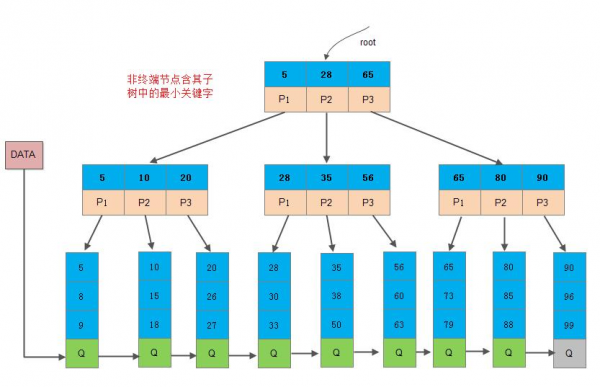
1. “关键字个数 = 子节点个数”，如下：【Mysql B+树实现】
   1. 【非终端节点（内部节点）包含其子树中的最大关键字】

      

   2. 【非终端节点（内部节点）包含其子树中的最小关键字】

      

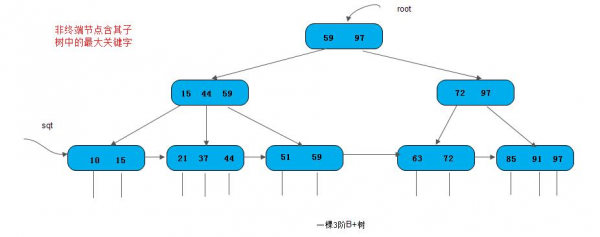
2. “关键字个数 = 子节点个数 - 1”，如下：【同 B树】
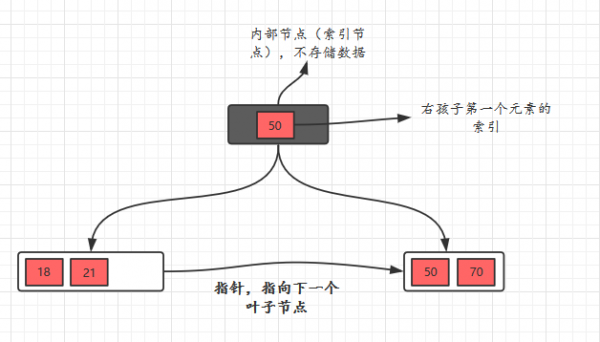
   • 【父节点存有右孩子的第一个元素的索引】

   

结构

B+树有两种类型的节点：内部结点（即：非叶子节点，也称“索引结点”）和叶子结点：

• 内部节点不存储数据，只存储索引，数据都存储在叶子节点。
• 所有结点（包括内部节点和叶子节点）中的 key 都按照从小到大的顺序排列。

  对于内部结点中的一个 key，左树中的所有 key 都小于它，右子树中的 key 都大于等于它。

• 每个叶子结点都存有相邻叶子结点的指针。
• 父节点存有右孩子的第一个元素的索引。【“关键字个数 = 子节点个数 - 1”时】

特点【相比于 B树】

1. 层级更少：B+树中间节点不保存数据，所以每个非叶子节点存储的关键字数更多，树的层级更少（I/O次数减少）所以查询数据更快；【B+树：叶子结点以上各层仅作为索引使用】
2. 查询速度稳定：B+树所有关键字数据地址都存在叶子节点上，导致每次查找的次数都相同，所以查询速度更稳定;【B+树：所有关键字都在叶子结点出现】
   • B树搜索有可能在非叶子结点结束。
3. 天然具备排序功能：B+树所有的叶子节点数据构成了一个有序链表，在范围查找时更方便，缓存的命中率更高。【B+树：叶子节点链表已有序】
4. 全节点遍历更快：B+树遍历整棵树只需要遍历所有的叶子节点即可，而不需要像B树一样需要对每一层进行遍历，这有利于数据库做全表扫描。
   • B树需要通过中序遍历获取。

B树 相对于 B+树 的优点是，如果经常访问的数据离根节点很近，这种时候检索可能会要比B+树快。

操作

查询

对 B+ 树可以进行两种查找运算：

1. 从最小关键字起顺序查找；【稠密索引，叶子节点有序】
2. 从根节点开始，进行随机查找；【稀疏索引，同B树查找类似，相当于“二分查找”】
   • 在查找时，若内部节点上的关键字等于给定值，并不终止，而是继续向下直到叶子节点。（内部节点只作为索引，而不保存值）

插入

插入过程中的分裂操作根据“关键字个数”与“子节点个数（子树个数）”关系的不同，略有差异。【】

• 插入的节点始终作为叶子节点，仅提取其关键字放到内部节点作为索引。

关键字最大值：

1. “关键字个数 = 子节点个数”，最大值为“m”；
2. “关键字个数 = 子节点个数 - 1”，最大值为“m”；

“关键字个数 = 子节点个数”

1. 如果为空树（当前节点是根节点）：创建一个叶子结点，然后将记录插入其中。
   • 此时这个叶子结点也是根结点。
2. 如果不为空树（当前节点非根节点）：
   1. 若插入后节点关键字个数 <= 关键字最大值，
   2. 若插入后节点关键字个数 > 关键字最大值，

“关键字个数 = 子节点个数 - 1”

1. 如果为空树（当前节点是根节点）：创建一个叶子结点，然后将记录插入其中。
   • 此时这个叶子结点也是根结点。
2. 如果不为空树（当前节点非根节点）：根据 key 值找到叶子结点，向这个叶子结点插入记录，
   1. 若插入后节点关键字个数 <= 关键字最大值，插入结束。【不可能被插入为“右侧子树的第一个元素”（小于索引就被插入到左侧树去了），所以不用考虑更新索引】
   2. 若插入后节点关键字个数 > 关键字最大值，将这个叶子结点以中间关键字为界分裂，并将“右侧子节点的第一个记录”的 key 进位到父结点（索引）中；再根据父节点（索引）关键字个数判断是否分裂。

“分裂”操作，示例：

1. 有 5 阶 B+树 如下：

   

2. 插入记录（关键字为16）：

   

3. 因为叶子节点的关键字个数 > 最大值（4），所以进行分裂：

   

   另一种分裂方式：给左结点3个记录，右结点2个记录，此时索引结点中的key就变为15。