树：B+树

来自Wikioe
跳到导航 跳到搜索


关于

B+树 是 B树 的一种变形形式，也是一种多路搜索树，但查询性能更好。

定义、结构、特点

B+树 特点是：能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度。

定义

基础定义与 B树 基本等价（包括关键字及子树的个数要求等）。


不同点：“关键字个数”与“子节点个数（子树个数）”，有两种不同的定义：

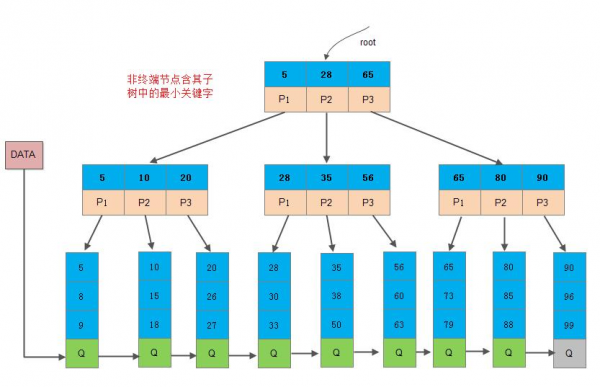
  1. “关键字个数 = 子节点个数”，如下：【Mysql B+树实现】
    1. 【非终端节点（内部节点）包含其子树中的最大关键字】
      B+树：“关键字个数 = 子节点个数”【非终端节点包含其子树中的最大关键字】.png
    2. 【非终端节点（内部节点）包含其子树中的最小关键字】
      B+树：“关键字个数 = 子节点个数”【非终端节点包含其子树中的最小关键字】.png
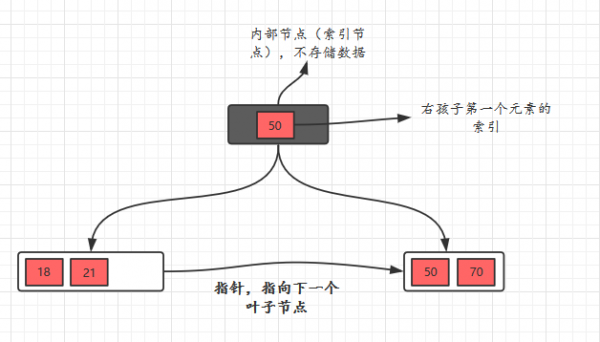
  2. “关键字个数 = 子节点个数 - 1”，如下：【同 B树】
    • 【父节点存有右孩子的第一个元素的索引】
    B+树：“关键字个数 = 子节点个数 - 1”【父节点存有右孩子的第一个元素的索引】.png

结构

B+树有两种类型的节点：内部结点（即：非叶子节点，也称“索引结点”）和叶子结点：

  • 内部节点不存储数据，只存储索引，数据都存储在叶子节点。
  • 所有结点（包括内部节点和叶子节点）中的 key 都按照从小到大的顺序排列。
    对于内部结点中的一个 key，左树中的所有 key 都小于它，右子树中的 key 都大于等于它。
  • 每个叶子结点都存有相邻叶子结点的指针。
  • 父节点存有右孩子的第一个元素的索引。【“关键字个数 = 子节点个数 - 1”时】
B+树：典型结构.png

特点【相比于 B树】

  1. 查询数据更快：B+树中间节点不保存数据，所以每个非叶子节点存储的关键字数更多，树的层级更少（I/O次数减少）所以查询数据更快；【B+树：叶子结点以上各层仅作为索引使用】
  2. 查询速度稳定：B+树所有关键字数据地址都存在叶子节点上，导致每次查找的次数都相同，所以查询速度更稳定;【B+树：所有关键字都在叶子结点出现】
    • B树搜索有可能在非叶子结点结束。
  3. 天然具备排序功能：B+树所有的叶子节点数据构成了一个有序链表，在范围查找时更方便，缓存的命中率更高。【B+树：叶子节点链表已有序】
  4. 全节点遍历更快：B+树遍历整棵树只需要遍历所有的叶子节点即可，而不需要像B树一样需要对每一层进行遍历，这有利于数据库做全表扫描。
    • B树需要通过中序遍历获取。


B树 相对于 B+树 的优点是，如果经常访问的数据离根节点很近，这种时候检索可能会要比B+树快。

操作

查询

对 B+ 树可以进行两种查找运算：

  1. 从最小关键字起顺序查找；【稠密索引，叶子节点有序】
  2. 从根节点开始，进行随机查找；【稀疏索引，同B树查找类似，相当于“二分查找”】
    • 在查找时，若内部节点上的关键字等于给定值，并不终止，而是继续向下直到叶子节点。（内部节点只作为索引，而不保存值）

插入

插入过程中的分裂操作根据“关键字个数”与“子节点个数（子树个数）”关系的不同，略有差异。【】

  • 插入的节点始终作为叶子节点，仅提取其关键字放到内部节点作为索引。


关键字最大值：

  1. “关键字个数 = 子节点个数”，最大值为“m”；
  2. “关键字个数 = 子节点个数 - 1”，最大值为“m”；

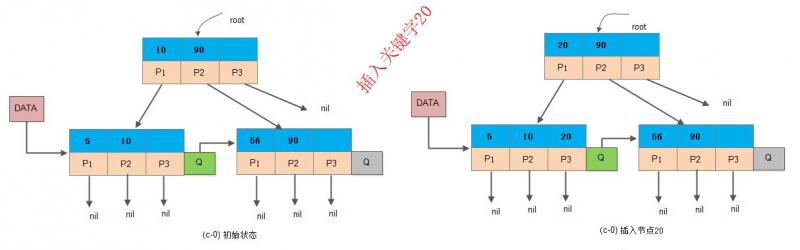
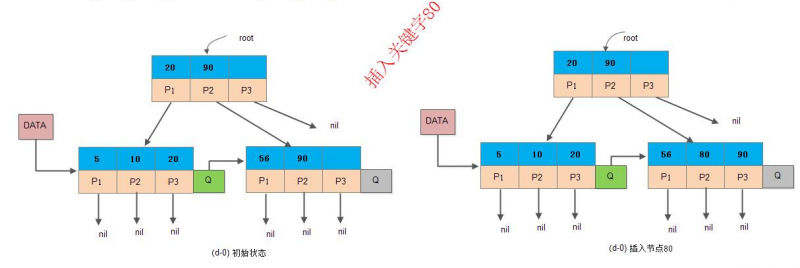
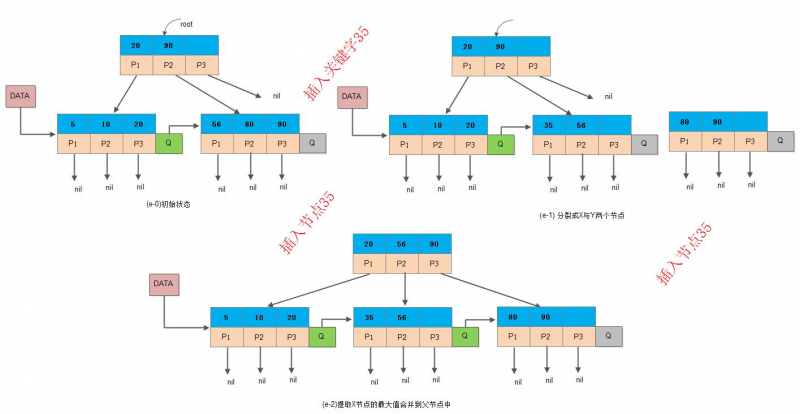
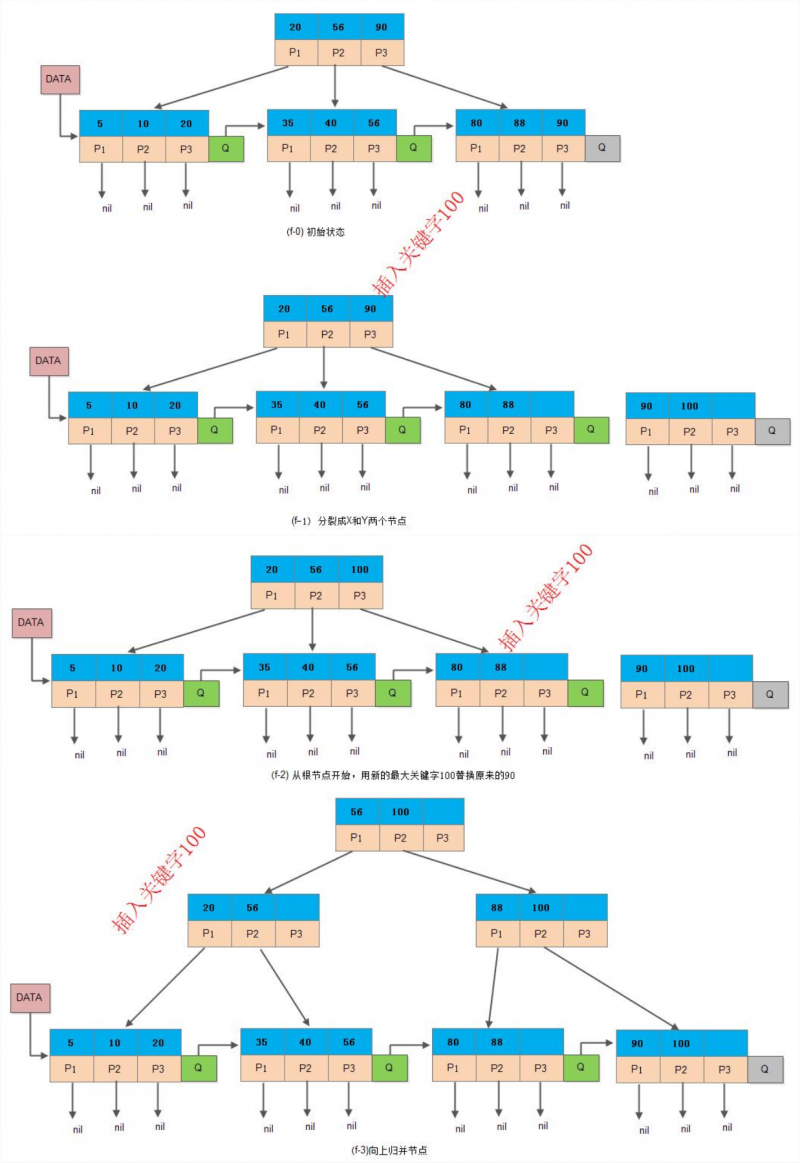
“关键字个数 = 子节点个数”

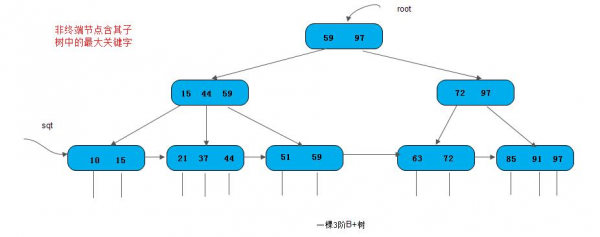
以【非终端节点（内部节点）包含其子树中的最大关键字】（子树最大关键字作为索引）为例：

  1. 如果当前节点是根节点：
    1. 若插入后节点关键字个数 <= 关键字最大值：直接插入。
      B+树：“关键字个数 = 子节点个数”插入根节点 1.png
    2. 若插入后节点关键字个数 > 关键字最大值：将节点分裂为两个新的叶子节点；并将两个新节点的最大关键字组合成为新的根节点。
      B+树：“关键字个数 = 子节点个数”插入根节点 2.png
  2. 如果不为空树（当前节点非根节点）：
    1. 若插入后节点关键字个数 <= 关键字最大值，
      1. 新插入记录的关键字是该叶子节点的最大关键字：使用该关键字作为“新索引”替换父节点中对应的关键字。
        B+树：“关键字个数 = 子节点个数”插入非根节点 1 1.png
      2. 新插入记录的关键字不是该叶子节点的最大关键字：直接插入。
        B+树：“关键字个数 = 子节点个数”插入非根节点 1 2.png
    2. 若插入后节点关键字个数 > 关键字最大值，将节点分裂为两个新的叶子节点（设为A、B），
      1. 新插入记录的关键字不是该叶子节点的最大关键字：提取“叶子节点A”的最大关键字作为“新增索引”合并到父节点。
        B+树：“关键字个数 = 子节点个数”插入非根节点 2 1.png
      2. 新插入记录的关键字是该叶子节点的最大关键字：使用该关键字作为“叶子节点B”的“新索引”替换父节点中对应的关键字，提取“叶子节点A”的最大关键字作为“新增索引”合并到父节点。
        B+树：“关键字个数 = 子节点个数”插入非根节点 2 2.png
  • 当更新了作为索引的关键字之后，内部节点的索引更新如上。

“关键字个数 = 子节点个数 - 1”

  1. 如果为空树（当前节点是根节点）：创建一个叶子结点，然后将记录插入其中。
    • 此时这个叶子结点也是根结点。
  2. 如果不为空树（当前节点非根节点）：根据 key 值找到叶子结点，向这个叶子结点插入记录，
    1. 若插入后节点关键字个数 <= 关键字最大值，插入结束。【不可能被插入为“右侧子树的第一个元素”（小于索引就被插入到左侧树去了），所以不用考虑更新索引】
    2. 若插入后节点关键字个数 > 关键字最大值，将这个叶子结点以中间关键字为界分裂，并将“右侧子节点的第一个记录”的 key 作为“新增索引”合并到父结点（索引）中；再根据父节点（索引）关键字个数判断是否分裂。


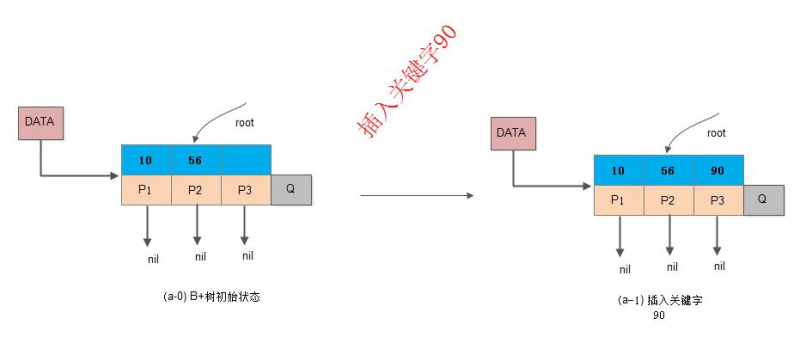
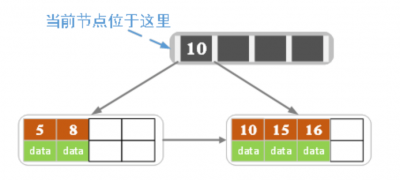
“分裂”操作，示例：

  1. 有 5 阶 B+树 如下：
    B+树：“关键字个数 = 子节点个数 - 1”插入：“分裂操作” 1.png
  2. 插入记录（关键字为16）：
    B+树：“关键字个数 = 子节点个数 - 1”插入：“分裂操作” 2.png
  3. 因为叶子节点的关键字个数 > 最大值（4），所以进行分裂：
    B+树：“关键字个数 = 子节点个数 - 1”插入：“分裂操作” 3.png
    另一种分裂方式：给左结点3个记录，右结点2个记录，此时索引结点中的key就变为15。

删除

B+树 的删除也仅在叶子节点中进行，因删除导致节点中关键字的个数少于最小关键字个数（m/2）时，其和兄弟节点的合并过程亦和 B树 类似。

  • “关键字个数 = 子节点个数 - 1”：删除操作后，叶子节点中的最大关键字在索引结点（内部节点）中的值可以作为一个分界关键字存在。
  • “关键字个数 = 子节点个数”：删除操作后，索引结点（内部节点）中存在的 key，不一定在叶子结点中存在对应的记录。

MySQL 中的应用

MySQL的数据存储在“data”目录下，“data”目录下的文件夹是以数据库为单位的，数据库文件夹下面存放的表数据。【“data/{数据库名}/表文件”】

  • 同一个数据库中，不同的表可以设置不同的存储引擎；
MySQL：不同存储引擎的表文件结构.png

MyISAM

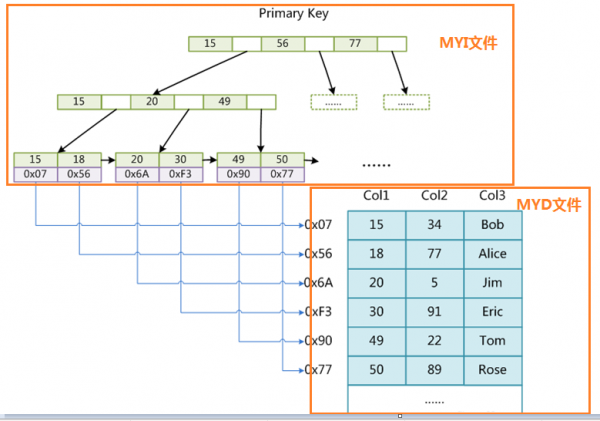
MyISAM 分别会存在一个“索引文件”（“*.MYI”）和“数据文件”（“*.MYD”）：【另有：“*.frm”存储表的结构】

  • 查询的时候，找到“索引文件”的叶子节点中保存的地址，然后通过地址在“数据文件”找到对应的信息。【“索引文件”的叶子节点指向“数据文件”真正数据记录】
MyISAM：文件结构.png


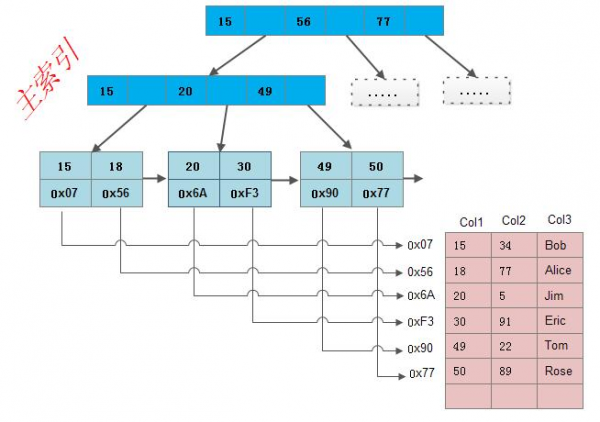
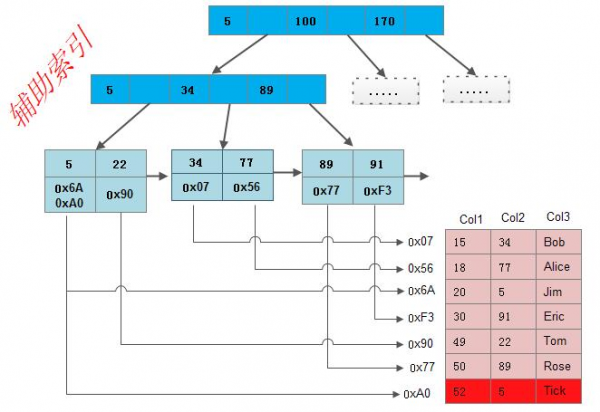
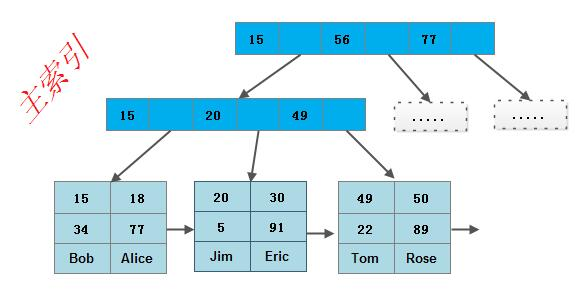
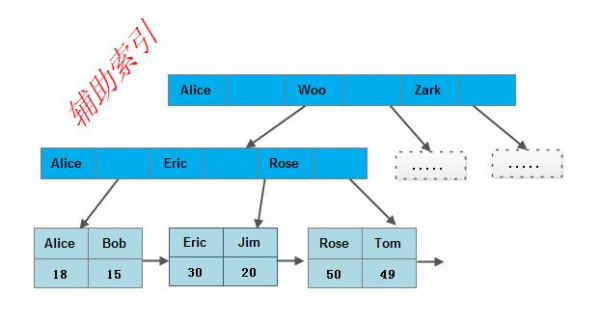
MyISAM 中有两种索引，分别是主索引和辅助索引：

  1. 主索引：使用具有唯一性（主键、唯一性约束的键）的键值进行创建；
  2. 辅助索引：键值可以是相同的。
MyISAM：主索引.png
MyISAM：辅助索引.png
  • 【MyISAM没有“聚集索引”】

InnoDB

InnoDB 和 MyISAM 的最大区别是它只有一个数据文件（“*.ibd”存储“索引和数据”）：【另有：“*.frm”存储表的结构】

  • 【“数据文件”本身按照 B+树 组织，其叶子节点就是数据记录】


InnoDB 也有两种索引：

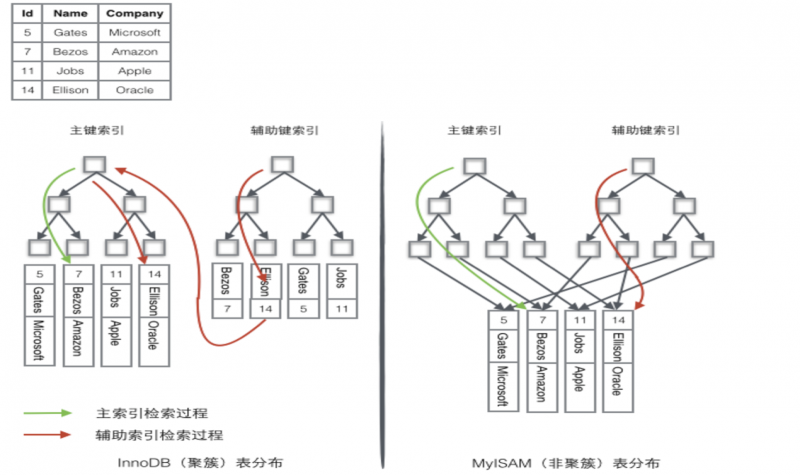
  1. 主索引：【聚集索引】，表数据文件本身就是一个索引结构（按 B+树 组织），这棵树的叶节点数据保存了完整的数据记录；
  2. 辅助索引：将主键作为数据域。
    • 辅助索引查找时：
      1. 通过辅助索引先找到主键，
      2. 然后通过主索引找到对应的主键，从而得到相应的数据信息（“回表”）。
InnoDB：主索引.png
InnoDB：辅助索引.png


MySQL 默认存储引擎 InnoDB 只显式支持B-Tree（从技术上来说是B+Tree）索引，对于频繁访问的表，InnoDB会透明建立“自适应hash索引”【InnoDB 的内存结构】，即在B树索引基础上建立hash索引，可以显著提高查找效率，对于客户端是透明的，不可控制的，隐式的。

关于聚簇索引与非聚簇索引

在《数据库原理》里面，对聚簇索引的解释是： 聚簇索引的顺序就是数据的物理存储顺序； 而对非聚簇索引的解释是：索引顺序与数据物理排列无关。

直观上来说，聚簇索引的叶子节点就是数据节点； 而非聚簇索引的叶子节点仍然是索引节点，只不过是指向对应数据块的指针。
索引对比：聚簇索引与非聚簇索引.png
  1. 聚集索引：【数据的索引】
    • 聚集索引的叶子节点存储表中所有的数据。
    • 一个表最多只能有一个聚簇索引。
    • 一个表必须有一个聚簇索引，即使你不创建主键，系统也会帮你创建一个隐式的主键作为聚簇索引。
      这是因为 InnoDB 是把数据存放在 B+ 树中的，而 B+ 树的键值就是主键，。
  2. 非聚集索引：【主键的索引】
    • （也称，辅助索引、二级索引）
    • 非聚集索引的叶子节点不存储表中的数据，而是存储该列对应的主键。
    • 查找数据时，先通过“非聚簇索引”找到“主键”，再根据主键去聚集索引中查找具体数据。【这个过程称为回表】

MySQL采用“B+树”原因

MySQL 等数据库普遍都采用“B+树”，而不是“B树”。主要有如下原因：【“B+树”相比于“B树”的特点】

  1. “B树”和“B+树”最重要的一个区别就是“B+树”只有叶子节点存放数据，其余节点用来索引。而“B树”是每个索引节点都会有 data 域。这就决定了“B+树”更适合用来存储外部数据。也就是所谓的磁盘数据。
  2. 从MySQL InnoDB的角度来看，“B+树”是用来充当索引的，一般来说索引非常大，尤其是关系型数据库这种数据量大的索引能达到亿级别，所以为了减少内存的占用，索引也会存储在磁盘上。
  3. “B+树”的磁盘读写代价更低。“B+树”的内部节点并没有指向关键字具体信息的指针，因此其内部节点相对“B树”更小。如果把所有同一内部节点的关键字存放在同一盘块中，那么盘块所能容纳的关键字数量也越多。一次性读入内存中的需要查找的关键字也就越多。相对来说IO读写次数也就降低了。
  4. “B+树”的查询效率更加稳定。由于非终节点并不是最终指向文件内容的节点，而只是叶子节点中关键字的索引。所以任何关键字的查找必须走一条从根节点到叶子节点的路。所有关键字查询的路径长度相同，导致每一个数据的查询效率相当。
  5. “B+树”所有的 Data 域在叶子节点，一般来说都会进行一个优化，就是将所有的叶子节点用指针串起来。这样遍历叶子节点就能获得全部数据，这样就能进行区间访问了。
取自“http://wiki.eijux.com/index.php?title=树：B%2B树&oldid=2755”