树（Tree）

关于“树”

在计算机科学中，树（tree）是一种抽象数据类型（ADT）。它是由 n（n>0）个有限节点组成一个具有层次关系的集合。

树具有以下的特点：

• 每个节点都只有有限个子节点或无子节点；
• 没有父节点的节点称为根节点；
• 每一个非根节点有且只有一个父节点；
• 除了根节点外，每个子节点可以分为多个不相交的子树；
• 树里面没有环路（cycle）

术语：

• 节点的度：一个节点含有的子树的个数称为该节点的度；
• 树的度：一棵树中，最大的节点度称为树的度；
• 叶节点（终端节点）：度为零的节点；
• 分支节点（非终端节点）：度不为零的节点；
• 父节点：若一个节点含有子节点，则这个节点称为其子节点的父节点；
• 子节点：一个节点含有的子树的根节点称为该节点的子节点；
• 兄弟节点：具有相同父节点的节点互称为兄弟节点；
• 其堂兄弟节点：父节点在同一层的节点互为堂兄弟；
• 节点的祖先：从根到该节点所经分支上的所有节点；
• 子孙：以某节点为根的子树中任一节点都称为该节点的子孙。
• 节点的层次：从根开始定义起，根为第 1 层，根的子节点为第 2 层，以此类推；
• 深度：从根到节点的唯一路径长。（根的深度为 0）
• 高度：从节点到其树叶的最长路径长。（所有树叶的高度为 0）
• 森林：由 m（m>=0）棵互不相交的树的集合称为森林；

树的种类：

1. 无序树：树中任意节点的子节点之间没有顺序关系，也称为自由树；
2. 有序树：树中任意节点的子节点之间有顺序关系；
   1. 二叉树：每个节点最多含有两个子树的树称为二叉树；
      1. 完全二叉树：对于一棵二叉树，假设其深度为 d（d > 1）。除了第 d 层外，其它各层的节点数目均已达最大值，且第 d 层所有节点从左向右连续地紧密排列；
         1. 满二叉树：所有叶节点都在最底层的完全二叉树；（最后一层子节点全满的特殊的完全二叉树）
      2. 平衡二叉树（AVL 树）：当且仅当任何节点的两棵子树的高度差不大于 1 的二叉树；
      3. 排序二叉树（二叉查找树，Binary Search Tree）：也称“二叉搜索树”、“有序二叉树”；
   2. 霍夫曼树：带权路径最短的二叉树称为“哈夫曼树”或“最优二叉树”；
   3. B 树：一种对读写操作进行优化的自平衡的二叉查找树，能够保持数据有序，拥有多于两个子树。【？？？B 树不是二叉树吧？？？】

二叉树

在计算机科学中，二叉树（Binary tree）是每个节点最多只有两个分支（即不存在分支度大于 2 的节点）的树结构。通常分支被称作“左子树”或“右子树”。二叉树的分支具有左右次序，不能随意颠倒。

• 二叉树的第“i”层至多拥有“2^(i-1)”个节点；
• 深度为“k”的二叉树至多总共有“2^(k+1)-1”个节点；

二叉树的遍历：

1. 深度优先（DFS）
   1. 先序（根）遍历（DLR）
   2. 中序（根）遍历（LDR）
   3. 后序（根）遍历（LRD）
2. 广度优先（BFS，即：层次遍历）

排序二叉树

---

排序二叉树, 又称为二叉查找树。其的特点:

• 一个节点左孩子的值, 一定小于它本身节点的值。
• 一个节点右孩子的值, 一定大于它本身节点的值。
• 左、右孩子（子树）也分别是排序二叉树。
• （没有键值相等的结点）

遍历方式的特点：【不同的遍历方式，有着不同的应用场景】

1. 先序：复制一个排序二叉树最快。【复制节点或树】
2. 中序：得到二叉树从小到大排序的数据。【获取序列】
3. 后序：执行操作时，肯定已经遍历过该节点的左右子节点，故适用于要进行破坏性操作的情况，比如删除所有节点。【文件系统常用】

排序二叉树体现了二分查找的思想，查找所需的最大次数等于二叉查找树的高度。

平衡二叉树

---

平衡二叉树（Balanced BinaryTree）又被称为AVL树。它具有以下性质：它是一棵空树或它的左右两个子树的高度差的绝对值不超过 1，并且左右两个子树都是一棵平衡二叉树。

• 平衡因子：节点的两个子树的高度差。（其绝对值必须小于等于 1，否则需要进行调整）

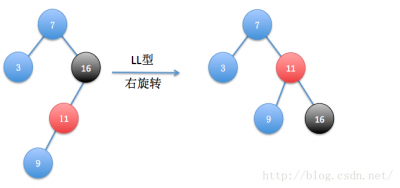
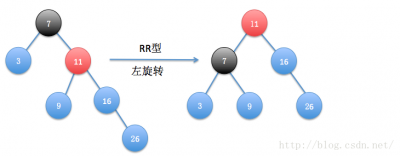
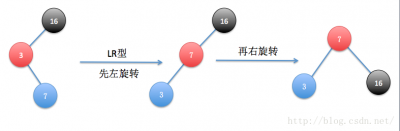
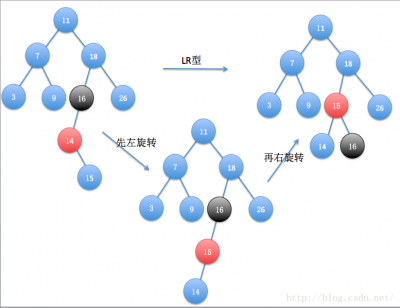
平衡的调整

平衡的调整通过对节点的旋转实现，共有四种情况：【L、R 代表“导致失衡的子节点”相对于“失衡节点”的位置，而非左旋或右旋的操作】

• （橘黄色的结点为旋转中心，黑色结点的为离插入结点最近的失衡结点）

1. LL：（左子树的左边节点）

   

   解决：右旋

2. RR：（右子树的右边节点）

   

   解决：左旋

3. LR：（左子树的右边节点）

   

   解决：先左旋再右旋

4. RL：（右子树的左边节点）

   

   解决：先右旋再左旋

红黑树

---

红黑树（Red Black Tree） 是一种含有红黑结点并能自平衡二叉查找树。

• 它可以在“O(log n)”时间内做查找，插入和删除（n 是树中元素的数目）。

Question：

1. 红黑树是平衡二叉树吗？

   红黑树是一种特化的 AVL树，但其并非严格的 AVL树，其平衡因子的绝对值可能大于 1。但对其进行平衡的代价较低，其平均统计性能要强于 AVL 。

2. 红黑树的应用？

   红黑树的应用十分广泛，如下：

   1. JDK 的集合类 TreeMap 和 TreeSet 底层实现，Java8 中 HashMap 的实现。
   2. Linux 的进程管理、内存管理，设备驱动及虚拟内存跟踪等一系列场景中。
   3. 一些数据库的索引实现等。

定义和性质

1. 每个节点要么是黑色，要么是红色。
2. 根节点是黑色。
3. 每个叶子节点（NIL）是黑色。
4. 每个红色结点的两个子结点一定都是黑色。【？】
   • 从每个叶子到根的所有路径上不能有两个连续的红色节点。
5. 任意一结点到每个叶子结点的路径都包含数量相同的黑结点。【？？？】
   • 如果一个结点存在黑子结点，那么该结点肯定有两个子结点。【所以，不存在只有一个叶子节点的节点？？？（因为叶子节点为黑色）】

这些规则限制保证了红黑树的自平衡。保证了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。【？？？】

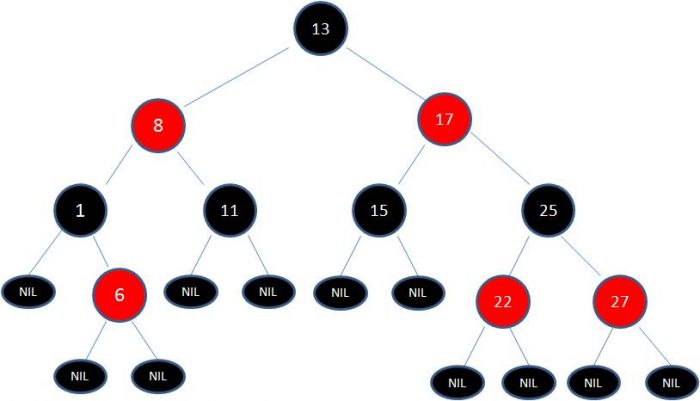
典型的红黑树，如图：

自平衡

红黑树总是通过旋转和变色达到自平衡。

• 旋转，包括“左旋”、“右旋”，与平衡二叉树同理。

操作

在进行“插入”和“删除”等可能会破坏树的平衡的操作时，需要进行自平衡以到平衡状态。

• “读取”操作与排序二叉树同理，不会对树结构造成破坏，所以不需要进行自平衡。

【红黑树的插入、删除包含很多种情况，每种情况有不同的处理方式，较为复杂（4种插入case和5种删除case）】

插入

插入的节点都是红色。原因如下：

1. 如果插入结点是红色：在父结点（如果存在）为黑色结点时，红黑树的黑色平衡没被破坏，不需要做自平衡操作。而在父结点（如果存在）为红色结点时，才需要自平衡。
2. 如果插入结点是黑色：那么插入位置所在的子树黑色结点总是多 1，必须做自平衡。

所有插入情景：

文件:红黑树插入操作结点的叫法约定.png

文件:红黑树插入情景.png

如上，情景1、2和3的处理很简单，而情景4.2和情景4.3只是方向反转而已。所以难点并不多。

---

---

---