树：R树

空间数据

基于实体的模型：

1. 0-dimensional objects：一般使用点point来表示那些对于不需要使用到形状信息的实体。
2. 1-dimensional objects or linear objects：用于表示一些路网的边，一般用于表示道路road。 (polyline)
3. 2-dimensional objects or surfacic objects：用于表示有区域面积的实体。 (polygon)

常用的空间数据查询方式：

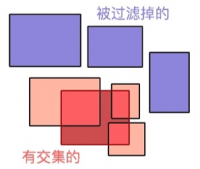
1. 窗口查询：给定一个查询窗口（通常是一个矩形），返回与查询窗口相重叠的物体。
2. 点查询：给定一个点，返回包含这个点的所有几何图形。

空间数据获取的方法

通常，我们不选择去索引几何物体本身，而是采用“最小限定箱”（MBB：minimum bounding box）作为不规则几何图形的 key 来构建空间索引：

1. 二维：称之为“最小限定矩形”（MBR：minimum bounding retangle）。

   

2. 三维：称之为“最小限定箱”（MBB：minimum bounding box）。

   

通过索引操作对象的 MBB 进行查询，步骤：【？？？】

1. Filtering：过滤掉 MBB 不相交的数据集，剩下的 MBB 被索引到的称为一个数据的超集。

   

2. Refinement：测试实际的几何形状会不会满足查询条件，精确化。

   

使用：

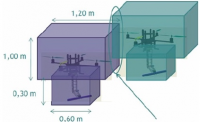
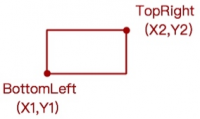
1. 用数据表示一个 MBR：

   通常，只需要两个点就可限定一个矩形，也就是矩形某个对角线的两个点（“左下右上”或“左上右下”）就可以决定一个唯一的矩形。

   

   1. 表示一个点的数据：

   　　　　public class Point{ //用一个类来表示一个点
   　　　　    public Float x;
   　　　　    public Float y
   　　　　}
   

   1. 表示一个 MBR 的数据：

   　　　　public class MBR{
   　　　　    public Point BottomLeft;
   　　　　    public Point TopRight;
   　　　　}
   

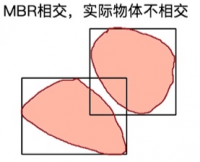
2. 判断两个 MBR 是否相交：

   如果一个MBR的TopLeft或者BottomRight的（x，y）位于另一个MBR的 xRange 和 yRangle 里面，则说明这两个MBR相交。

   

R树

简介

R树 是 B树 在高维空间的扩展：采用 B树 分割空间的思想，并在添加、删除操作时采用合并、分解结点的方法，保证树的平衡性。因此，R树就是一棵用来存储高维数据的平衡树。

每个 R树 的叶子结点包含了多个指向不同数据的指针，这些数据可以是存放在硬盘中的，也可以是存在内存中。

根据 R树 的这种数据结构，当需要进行一个高维空间查询时，只需要遍历少数几个叶子结点所包含的指针，查看这些指针指向的数据是否满足要求即可。

1984年，加州大学伯克利分校的Guttman发表了一篇题为“R-trees: a dynamic index structure for spatial searching”的论文，向世人介绍了R树这种处理高维空间存储问题的数据结构。
* Guttman, A.; “R-trees: a dynamic index structure for spatial searching,” ACM, 1984, 14

R树在现实领域中能够解决的例子：查找20英里以内所有的餐厅。

1. 如果没有 R树 怎么解决？

   一般情况下我们会把餐厅的坐标“(x,y)”分为两个字段存放在数据库中，一个字段记录经度，另一个字段记录纬度。这样的话我们就需要遍历所有的餐厅获取其位置信息，然后计算是否满足要求。

   如果一个地区有100家餐厅的话，我们就要进行100次位置计算操作了，如果应用到谷歌地图这种超大数据库中，这种方法便必定不可行了。

2. R树 的解决？

   R树采用了一种称为“MBR”（Minimal Bounding Rectangle，即最小边界矩形）的方法对空间进行分割……

   R树 使我们不必遍历所有数据即可获得答案，效率显著提高。

   如下：

引子

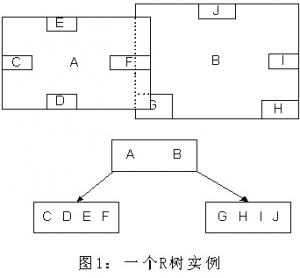
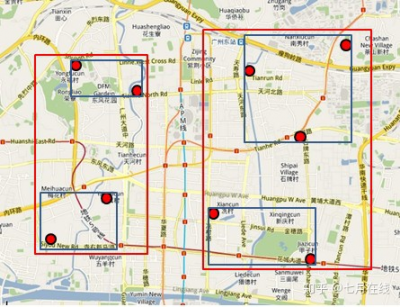
R树 示例：

R树 采用了一种称为“MBR”对空间进行分割：从叶子结点开始用矩形（rectangle）将空间框起来，结点越往上，框住的空间就越大，以此对空间进行分割。

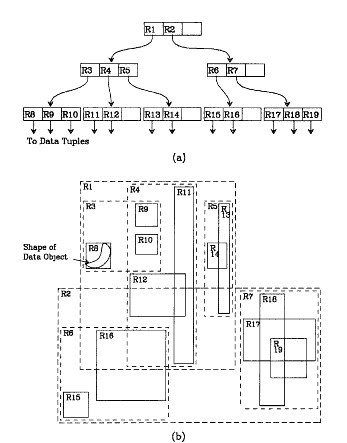
“MBR”分割示例：（假设所有数据都是二维空间下的点）

1. 如图，“shape of data object”所标记的是一块不规则图形，我们把它看作是多个数据围成的一个区域。为了实现“R树”结构，用一个最小边界矩形恰好框住这个不规则区域，这样就构造出了一个区域：“R8”。

   其他实线包围住的区域（“R8”到“R19”）同理。【这些矩形都将被存储在页子结点】

2. 如图，可以发现“R8”，“R9”，“R10”三个矩形距离最为靠近，因此就可以用一个更大的矩形“R3”恰好框住这 3 个矩形。【叶子节点的父节点】

   同理：“R15”，“R16”被“R6”恰好框住；“R11”，“R12”被“R4”恰好框住，等等。

3. 重复上一步，所有最基本的最小边界矩形被框入更大的矩形中之后，再次迭代，用更大的框去框住这些矩形。

最后，根结点存放的是两个最大的矩形，这两个最大的矩形框住了所有的剩余的矩形，当然也就框住了所有的数据。

• 下一层的结点存放了次大的矩形，这些矩形缩小了范围。
• 每个叶子结点都是存放的最小的矩形，这些矩形中可能包含有n个数据。

对应于地图的情况：

1. 打开地图（也就是整个R树），先选择国内还是国外，【对应根结点】
2. 然后选择华南地区（对应第一层结点），选择广州市，【对应第二层结点】
3. 再选择天河区，【对应第三层结点】
4. 最后选择天河城所在的那个区域。【对应叶子结点，存放有最小矩形】

如图：

定义（性质）

---

1. 非根非叶子结点拥有“m”至“M”个子结点（子树）。【？？？】
2. 叶子结点包含有“m”至“M”个记录索引（条目）。作为根结点的叶子节点所具有的记录个数可以少于“m”。通常，“m=M/2”。【？？？】
3. 对于节点（叶子、非叶子节点）的所有记录（条目），“I”是最小的可以在空间中完全覆盖这些记录所代表的点的矩形（“矩形”是可以扩展到高维空间的）。
4. 所有叶子结点都位于同一层，因此 R树 为平衡树。

结构

---

如图，“R树的节点存储结构”：

叶子结点

叶子结点所保存的数据形式为：“(I, tuple-identifier)”，其中：

1. “I”：是一个 n 维空间的矩形，并可以恰好框住这个叶子结点中所有记录代表的 n 维空间中的点。【框住点的最小矩形，如引子中的“R8”】

   如：“I=(I0,I1,…,In-1)”。

2. “tuple-identifier”：表示的是一个存放于数据库中的 tuple（多元组），也就是一条记录，它是 n 维的。【所有的点，如引子中构成“shape of data object”的所有点】

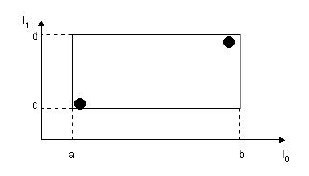
示例，在二维空间中的叶子结点所要存储的信息：

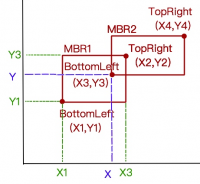
如图，

1. “I”所代表的就是图中的矩形，其范围是“a<=I0<=b”，“c<=I1<=d”。
2. “tuple-identifier”，在图中即表示为那两个点。

• 这种形式完全可以推广到高维空间。

非叶子结点

非叶子结点存放的数据结构为：“(I, child-pointer)”，其中：

1. “I”：覆盖所有孩子结点对应矩形的矩形。【框住所有孩子节点矩形的最小矩形，如如引子的“R3”】

   如：“I=(I0,I1,…,In-1)”。

2. “child-pointer”：表示指向孩子结点的指针。

---

---

---

参考

1. 空间数据索引RTree（R树）完全解析及Java实现
2. 从B树、B+树、B*树谈到R 树
3. 什么是R树？