树：红黑树

来自Wikioe
跳到导航 跳到搜索


关于

红黑树（Red Black Tree） 是一种含有红黑结点并能自平衡二叉查找树。

  • 它可以在“O(log n)”时间内做查找，插入和删除（n 是树中元素的数目）。


Question：

  1. 红黑树是平衡二叉树吗？
    红黑树是一种特化的 AVL树，但其并非严格的 AVL树，其平衡因子的绝对值可能大于 1。但对其进行平衡的代价较低，其平均统计性能要强于 AVL 。
  2. 红黑树的应用？
    红黑树的应用十分广泛，如下：
    1. JDK 的集合类 TreeMap 和 TreeSet 底层实现，Java8 中 HashMap 的实现。
    2. Linux 的进程管理、内存管理，设备驱动及虚拟内存跟踪等一系列场景中。
    3. 一些数据库的索引实现等。

定义和性质

  1. 每个节点要么是黑色，要么是红色。
  2. 根节点是黑色。
  3. 每个叶子节点（NIL）是黑色。
    • 【图中未必画出，但叶子节点都是“NULL”指针。】
  4. 每个红色结点的两个子结点一定都是黑色。【？】
    • 从每个叶子到根的所有路径上不能有两个连续的红色节点。
  5. 任意一结点到每个叶子结点的路径都包含数量相同的黑结点。【？？？】
    • 如果一个结点存在黑子结点，那么该结点肯定有两个子结点。【所以，不存在只有一个叶子节点的节点？？？（因为叶子节点为黑色）】

这些规则限制保证了红黑树的自平衡。保证了红黑树的关键性质: 从根到叶子的最长的可能路径不多于最短的可能路径的两倍长。【？？？】


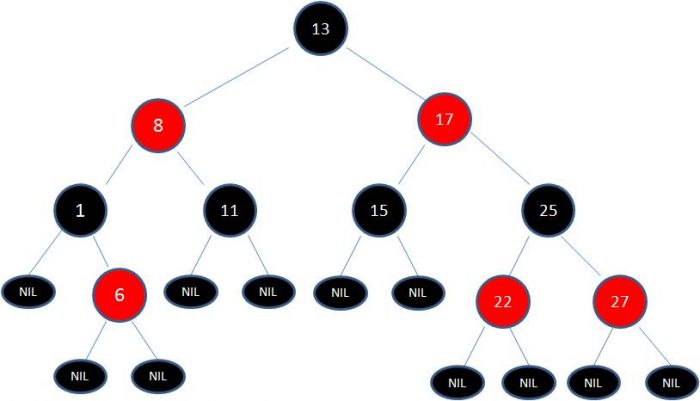
典型的红黑树，如图：

典型的红黑树.jpg

自平衡

红黑树总是通过旋转和变色达到自平衡。

  • 旋转，包括“左旋”、“右旋”，与平衡二叉树同理。

操作

在进行“插入”和“删除”等可能会破坏树的平衡的操作时，需要进行自平衡以到平衡状态。

  • “读取”操作与排序二叉树同理，不会对树结构造成破坏，所以不需要进行自平衡。

【红黑树的插入、删除包含很多种情况，每种情况有不同的处理方式，较为复杂（4种插入case和5种删除case）】

插入

插入操作包括两部分工作：

  1. 查找插入的位置；
  2. 插入后自平衡。

查找插入的父结点很简单，跟查找操作区别不大。重点在于自平衡。


  • 插入的节点都是红色。原因如下：
    1. 如果插入结点是红色：在父结点（如果存在）为黑色结点时，红黑树的黑色平衡没被破坏，不需要做自平衡操作。而在父结点（如果存在）为红色结点时，才需要自平衡。
    2. 如果插入结点是黑色：那么插入位置所在的子树黑色结点总是多 1，必须做自平衡。
  • 红黑树的生长是自底向上的。从插入节点开始，向上作自平衡处理。（这点不同于普通的二叉查找树，其生长是自顶向下的）


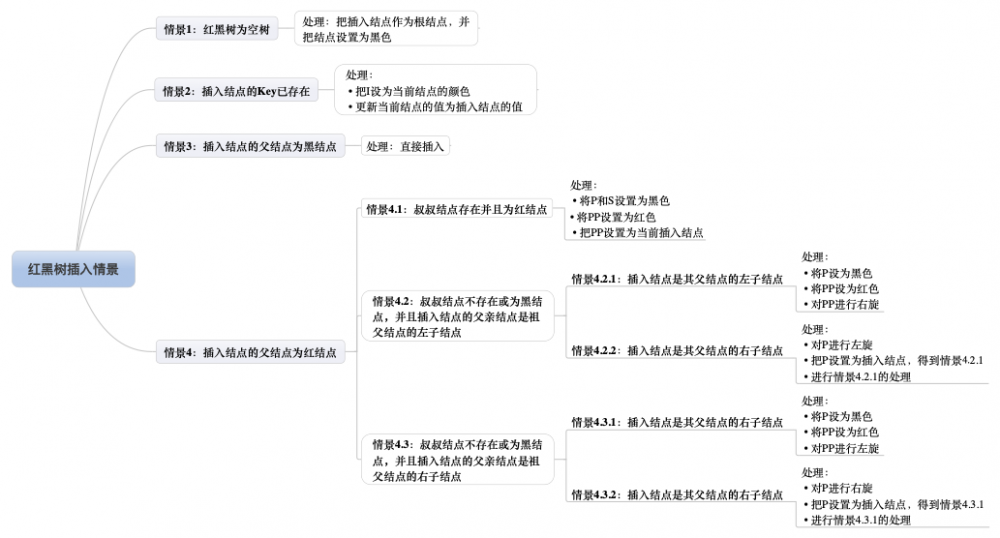
所有插入情景：

红黑树：插入操作结点的叫法约定.png
红黑树：插入情景.png

如上，情景1、2和3的处理很简单，而情景4.2和情景4.3只是方向反转而已。所以难点再“插入结点的父结点为红结点”时：

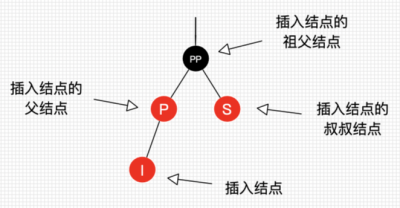
如果插入的父结点为红结点，那么该父结点不可能为根结点，所以插入结点总是存在祖父结点。这点很重要，因为后续的旋转操作肯定需要祖父结点的参与。


情景4.1：父结点为红结点，叔叔结点存在并且为红结点

从红黑树“性质4”（不可以同时存在两个相连的红结点）可以确定：祖父结点肯定为黑结点。

那么此时该插入子树的红黑层数的情况是：黑红红，显然最简单的处理方式是把其改为：红黑红：

  1. 将 P 和 S 设置为黑色；
  2. 将 PP 设置为红色；
    如图：
    红黑树：插入情景4.1 1.png 红黑树：插入情景4.1 2.png
  3. 把 PP 设置为当前插入结点：【此时 PP 结点为红色】
    1. 如果 PP 的父结点是黑色，则已平衡无需再处理；
    2. 如果 PP 的父结点是红色（“性质4”），则把 PP 当作新的插入结点，应用不同插入情景继续插入操作自平衡处理；
    3. 如果 PP 刚好为根结点时（“性质2”），必须把 PP 重新设为黑色，那么树的红黑结构变为：黑黑红。
      即，从根结点到叶子结点的路径中，黑色结点增加了。【这是唯一一种会增加红黑树黑色结点层数的插入情景】

情景4.2：父结点为红结点，叔叔结点不存在或为黑结点，父结点是祖父结点的左子结点

从红黑树“性质5”（任意一结点到每个叶子结点的路径都包含数量相同的黑结点）可以确定：叔叔结点非红即为叶子结点（NIL）。

因为如果叔叔结点为非叶子节点的黑结点，而父结点为红结点，那么叔叔结点所在的子树的黑色结点就比父结点所在子树的多了，这不满足红黑树的“性质5”。


分为两种情况：

  1. 情景 4.2.1：“插入结点是其父结点的左子结点”，处理：
    1. 将 P 设为黑色；【此时，叔叔节点不存在，或为叶子节点（黑色）】
    2. 将 PP 设为红色；
    3. 对 PP 进行右旋。
    红黑树：插入情景4.2.1.png
    如上，已平衡无需再处理。
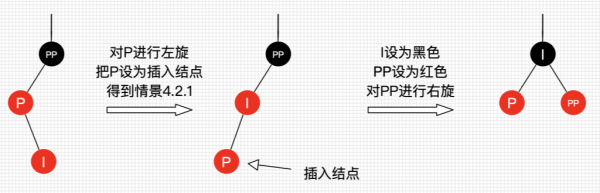
  2. 情景 4.2.2：“插入结点是其父结点的右子结点”，处理：
    1. 对 P 进行左旋；
    2. 把 P 设置为插入结点，得到“情景 4.2.1”，并进行如上“情景4.2.1”处理。
    红黑树：插入情景4.2.2.png

情景4.3：父结点为红结点，叔叔结点不存在或为黑结点，父结点是祖父结点的右子结点【类似“情景4.2”】

【同上“情景4.2”，只是方向不同，对应的旋转操作不同】 分为两种情况：

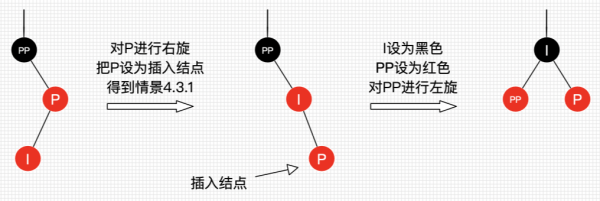
  1. 情景 4.3.1：“插入结点是其父结点的左子结点”，处理：
    1. 将 P 设为黑色；
    2. 将 PP 设为红色；
    3. 对 PP 进行左旋。
    红黑树：插入情景4.3.1.png
    如上，已平衡无需再处理。
  2. 情景 4.3.2：“插入结点是其父结点的右子结点”，处理：
    1. 对 P 进行左旋；
    2. 把 P 设置为插入结点，得到“情景 4.3.1”，并进行如上“情景4.3.1”处理。
    红黑树：插入情景4.3.2.png

删除

删除操作也包括两部分工作：

  1. 查找目标结点；
    • 当不存在目标结点时，忽略本次操作；
  2. 删除后自平衡。
    • 删除结点后还需要找结点来替代被删除结点的位置：
    1. 被删除结点无子结点，直接删除；
    2. 被删除结点仅一个子结点，用子结点替换删除结点；
    3. 被删除结点有两个子结点，用后继结点替换删除结点；【后继结点（中序遍历的后继节点）。即：大于删除结点的最小结点。】


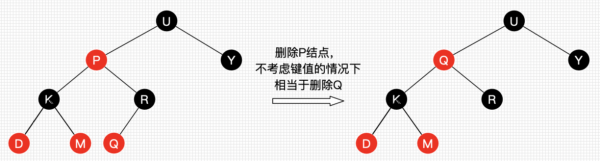
删除思路：删除结点被替代后，在不考虑结点的键值的情况下，对于树来说，可以认为删除的是替代结点。如图：

红黑树：删除结点换位思路.png

所以，如上三种替代节点情况都可以转换：

  1. “被删除结点仅一个子结点”：可以看作“删除子节点”。如果子节点又有两个子节点（对于红黑树，不可能子节点只有一个子节点），则相当于删除节点时“被删除结点有两个子结点”。
  2. “被删除结点有两个子结点”：可以看作“删除后继节点”。如果后继结点有右子结点（肯定不存在左结点？？？），则相当于删除节点时“被删除结点仅一个子结点”。

如上图，删除“P”（有两个子节点），可以看作删除“P”的后继节点“Q”

红黑树：二叉树删除情景转换.png

综上所述，删除操作删除的结点可以看作删除替代结点，而替代结点最后（经过层层的删除情景转换）总是在树末。

所以，删除红黑树的情景就少了很多，只需考虑删除树末结点的情景了。


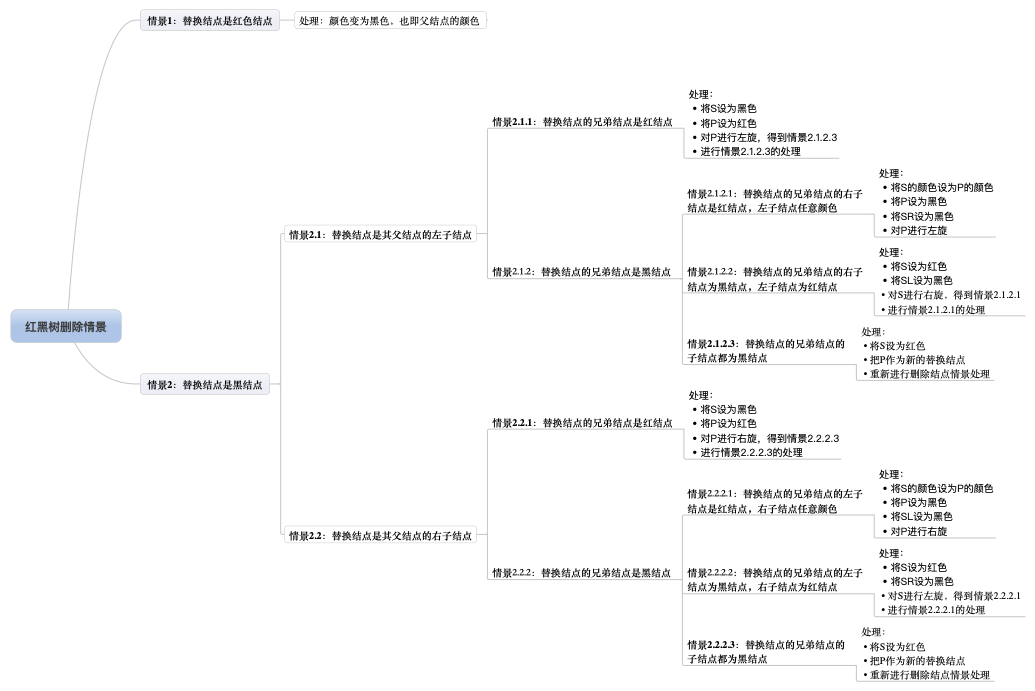
所有删除情景：

红黑树：删除操作结点的叫法约定.png
红黑树：删除情景.png

情景1：替换结点是红色结点

把替换结点换到了删除结点的位置时，由于替换结点时红色，删除也了不会影响红黑树的平衡，只要把替换结点的颜色设为被删除的结点的颜色即可重新平衡。

情景2：替换结点是黑结点

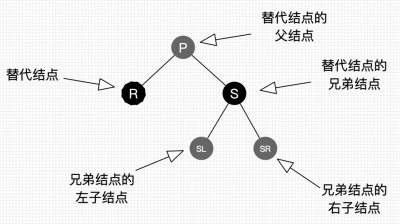
当替换结点是黑色时，就不得不进行自平衡处理了。我们必须还得考虑替换结点是其父结点的左子结点还是右子结点，来做不同的旋转操作，使树重新平衡。

情景2.1：替换结点是黑结点，替换结点是其父结点的左子结点

分为两种情况：

  1. 情景2.1.1：“替换结点的兄弟结点是红结点”，处理：
    • 若兄弟结点是红结点，那么根据“性质4”，兄弟结点的父结点和子结点肯定为黑色。
    1. 将 S 设为黑色；
    2. 将 P 设为红色；
    3. 对P进行左旋，得到“情景2.1.2.3”并处理。
    红黑树： 删除情景2.1.1.png
  2. 情景2.1.2：“替换结点的兄弟结点是黑结点”，处理：
    • 当兄弟结点为红结点，其父结点和子结点的具体颜色无法确定。此时又得考虑多种情景：
    1. “情景2.1.2.1”：“替换结点的兄弟结点的右子结点是红结点，左子结点任意颜色”，处理：
      • 即将删除的左子树的一个黑色结点【R 结点】，显然左子树的黑色结点少 1 了，然而右子树又又红色结点，那么我们直接向右子树“借”个红结点来补充黑结点就好啦，此时肯定需要用旋转处理了。
      1. 将 S 的颜色设为 P 的颜色；
      2. 将 P 设为黑色；
      3. 将 SR 设为黑色；
      4. 对 P 进行左旋。
      红黑树：删除情景2.1.2.1.png
      【如上，平衡后的图看似不满足红黑树的性质（性质5）：R 是即将替换的，它还参与树的自平衡，平衡后再替换到删除结点的位置，即 R 最终可以看作是删除的。所以最终仍是满足红黑树性质的。】
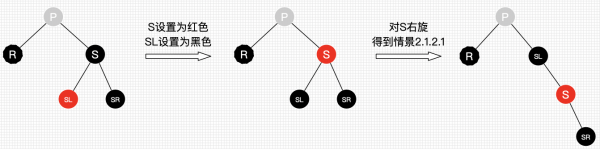
    2. “情景2.1.2.2”：“替换结点的兄弟结点的右子结点为黑结点，左子结点为红结点”，处理：
      • 兄弟结点【S 结点】所在的子树有红结点，我们总是可以向兄弟子树借个红结点过来，显然该情景可以转换为“情景2.1.2.1”。
      1. 将 S 设为红色；
      2. 将 SL 设为黑色；
      3. 对 S 进行右旋，得到“情景2.1.2.1”。
      红黑树：删除情景2.1.2.2.png
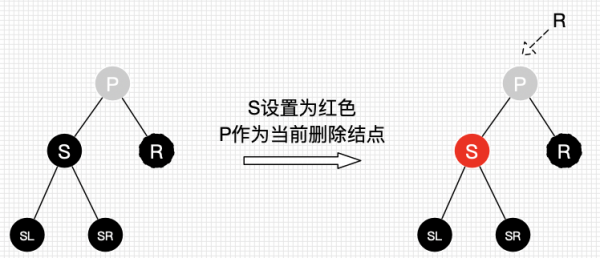
    3. “情景2.1.2.3”：“替换结点的兄弟结点的子结点都为黑结点”，处理：
      • 兄弟子树没有红结点可“借”时：把兄弟结点设为红色，再把父结点当作替代结点，去向父结点的兄弟结点去“借”，而后再进行平衡。【把兄弟结点设为红色，是为了在 P 所在的子树中保证平衡（R 即将删除，少了一个黑色结点，子树也需要少一个）】
      1. 将 S 设为红色；
      2. 把 P 作为新的替换结点；
      3. 重新应用删除结点情景来进行处理。
      红黑树：删除情景2.1.2.3.png
情景2.2：替换结点是黑结点，替换结点是其父结点的右子结点【类似“情景2.1”】

【同上“情景2.1”，只是方向不同，对应的旋转操作不同】

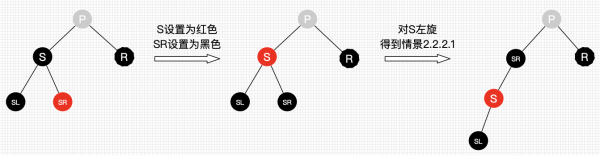
  1. 情景2.2.1：“替换结点的兄弟结点是红结点”，处理：
    1. 将 S 设为黑色；
    2. 将 P 设为红色；
    3. 对P进行右旋，得到“情景2.2.2.3”并处理。
    红黑树：删除情景2.2.1.png
  2. 情景2.2.2：“替换结点的兄弟结点是黑结点”：
    1. “情景2.2.2.1”：“替换结点的兄弟结点的左子结点是红结点，右子结点任意颜色”，处理：
      1. 将 S 的颜色设为 P 的颜色；
      2. 将 P 设为黑色；
      3. 将 SL 设为黑色；
      4. 对 P 进行右旋。
      红黑树：删除情景2.2.2.1.png
    2. “情景2.2.2.2”：“替换结点的兄弟结点的左子结点为黑结点，右子结点为红结点”，处理：
      1. 将 S 设为红色；
      2. 将 SR 设为黑色；
      3. 对 S 进行左旋，得到“情景2.2.2.1”。
      红黑树：删除情景2.2.2.2.png
    3. “情景2.2.2.3”：“替换结点的兄弟结点的子结点都为黑结点”，处理：
      1. 将 S 设为红色；
      2. 把 P 作为新的替换结点；
      3. 重新应用删除结点情景来进行处理。
      红黑树：删除情景2.2.2.3.png
取自“http://wiki.eijux.com/index.php?title=树：红黑树&oldid=2571”