核心技术:基本程序设计结构
跳到导航
跳到搜索
数据类型
| 类型 | 存储需求 | 默认值 | 取值范围 |
|---|---|---|---|
| 整型 | |||
| int | 4字节 | 0 | -2 147 483 648 - 2 147 483 647
|
| short | 2字节 | 0 | -32 768 - 32767
|
| long | 8字节 | 0L | -9 223 372 036 854 775 808 - 9 223 372 036 854 775 807
|
| byte | 1字节 | 0 | -128 - 127
|
| 浮点 | |||
| float | 4字节 | 0.0f | 大约 +- 3.402 823 47E+38F(有效位数为6、7位)
|
| double | 8字节 | 0.0d | 大约 +- 1.797 693 134 862 315 70E+308(有效位数为15位)
|
| 字符 | |||
| char | 2字节 | 'u0000' | \u0000 - \uffff |
| 布尔 | |||
| boolean | 1位 | false | true | false |
- 常量“Double.POSITIVE_INFINITY”、“Double.NEGATIVE_INFINITY”、“Double.NAN”分别表示“正无穷大”、“负无穷大”、“NaN(不是一个数字)”;
取值范围
- 整数用原码,负数用补码表示
以int为例,在java中占4字节,即32位:
- 其中第一位为符号位(0正,1负)
- 所以负数范围为:-2^31 = -2147483648
- 整数的范围为:2^31-1 = 2147483647 (减去全为0时的情况,0无正负)
即:-2147483648 - 2147483647 (-2^31 — 2^31-1)
关于0.2 + 0.1 不等于 0.3
使用自然类型计算小数的时候,会出现:“0.2+0.1=0.30000000000000004”,而“0.1+0.6=0.7”的情况:
其原因如下:
计算机存储、计算或者展示,都需要转换2进制。 在现实世界中,数字主要有整数和小数两种,整数包括正整数、负整数以及零。 计算机中表示整数的方式有很多,如原码、反码以及补码等。 在计算机中存储的整数则分为有符号数和无符号数。 对于无符号数,采用哪种编码方式都无所谓,对于有符号数的编码方式,常用的是补码。 那么,一个十进制数字想要获得其二进制的补码,需要先通过一定的算法得到他对应的原码。
- 十进制整数转换为二进制,可以采用“除2取余,逆序排列”,或者xxx法(列出“...128,64,32,26,8,4,2,1”,根据十进制数在对应位置1或0);
- 十进制小数转换为二进制:则采用“乘2取整,顺序排列”的方法;
如,0.625的二进制转换如下:

而0.1的二进制:
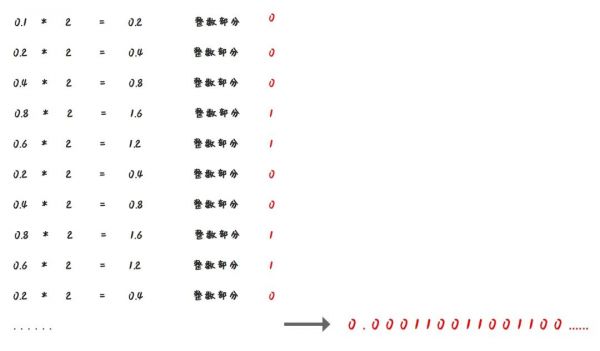
可以得知:0.1的二进制转换中出现了无限循环的情况,也就是(0.1)10 = (0.000110011001100…)2,而不能把0.1转换为确定的二进制数
即计算机无法用二进制精确的表示0.1
IEEE 754规定了四种表示浮点数值的方式:单精确度(32位)、双精确度(64位)、延伸单精确度(43比特以上,很少使用)与延伸双精确度(79比特以上,通常以80位实现)
但仅是用近似值表示小数,并非真实值,如果使用float、double等类型进行小数计算,仍然会丢失数值。并没有解决问题。
所以:为了解决这样的精度问题,Java中提供了BigDecimal来进行精确运算。
- BigDecimal 并不是Java的数据类型,而是一个Java对象!
变量
- 变量名:以字母开头,并由字母和数字构成的序列;(字母包括:'A'-'Z'、'a'-'z'、'_'、'$'、'ä')
- 不能使用java保留字作为变量名;
- 变量名对大小写敏感;
常量
- java 中利用关键字“final”指示常量;(表示变量只能被赋值一次)
- 习惯上,常量名使用全大写;
- 如果需要某个常量在一个类的多个方法中使用,则将其设置为类常量,用“static final”修饰;