树：B树

关于

B树（B-tree）和平衡二叉树稍有不同，属于多叉树又名平衡多路查找树（查找路径不只两个），数据库索引技术里大量使用者 B树 和 B+树 的数据结构。

Question：

1. B树 为什么是多叉而非二叉？

   B 树是为了磁盘或其它存储设备而设计的一种多叉。

   如果使用二叉树，在信息量很大的情况下，树的高度势必十分巨大，而层数越多读取时的I/O次数也就越多，大大降低了效率。

   如果使用多叉树，其实际的比较操作并不少，但是内容中的对比其消耗很小；而树的高度足够低，I/O操作足够少，就可以提升查找性能。

2. B树 属于一种“2-3树”？

   【……】

定义和性质

B树 的一个重要概念是“阶数（m）”表示该树每个节点最多有 m 个子树。

• 当 m 取 2 时，就是常见的二叉搜索树。
• “m 阶B树”，不等同于“m 叉树”。

在实际应用中的 B 树的阶数 m 都非常大（通常大于100），所以即使存储大量的数据，B 树的高度仍然比较小。

定义：【注意关键字与子树的不同】
（一颗 m 阶的 B 树）

1. 每个结点最多有“m-1”个关键字；【每个结点最多有m个子树】
2. 根结点至少有 1 个关键字；【根结点至少有2个子树】
3. 非根非叶子结点至少有“m/2”个关键字；【非根非叶子结点至少有“ceil(m/2)”个子树】
4. 每个结点中的关键字都按照从小到大的顺序排列，每个关键字的左子树中的所有关键字都小于它，而右子树中的所有关键字都大于它；
5. 所有叶子结点都位于同一层；【即：根结点到每个叶子结点的长度都相同】

Note：

• “ceil”为向上取整，如“ceil(m/2)=3”。
• B 树中的每个节点由两部分组成：
  1. 关键字（可以理解为数据）
  2. 指向孩子节点的指针

特点：
B 树的每个节点可以表示的信息更多，因此整个树更加“矮胖”，这在从磁盘中查找数据（先读取到内存、后查找）的过程中，可以减少磁盘 IO 的次数，从而提升查找速度。

关于关键字

（由上述定义可知）

1. 根节点的关键字数量范围：“1 <= k <= m-1”；
2. 非根节点的关键字数量范围：“m/2 <= k <= m-1”；
3. 【？？？】叶子结点不包含关键字。【可以把叶子结点看成在树里实际上并不存在外部结点，指向这些外部结点的指针为空】
   • 叶子结点的数目正好等于树中所包含的关键字总个数加 1。

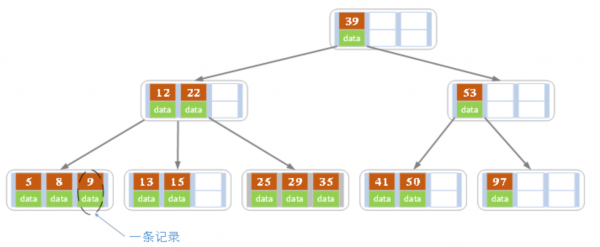
如：一个 4 阶的B树，根节点的关键字个数：1 <= k <= 3，非根节点的关键字个数：2 <= k <= 3。

• 关键字与子树：N 个关键字可以确定 N+1 个范围（即，N+1 个子树），所以【“节点的子树个数”=“节点的关键字个数”+ 1】。
  • 阶数为该树的子树的最大值。

Note：

• 每个结点中存储了关键字（key）和关键字对应的数据（data），以及孩子结点的指针。我们将一个 key 和其对应的 data 称为一个记录。
• 在数据库中将 B 树（和 B+ 树）作为索引结构，此时 B 树中的 key 就表示键，而 data 表示了这个键对应的条目在硬盘上的逻辑地址。

B 树的平衡：

B 树的平衡条件则有三点：

1. 叶子节点都在同一层；
2. 每个节点的关键字数为子树个数减一；
3. 节点的关键字有序；

如果要添加数据的子树的关键字数已经是最多，就需要拆分节点，调整树的结构。

操作

查询

从根节点开始：

1. 对节点内的关键字序列（有序）进行二分查找，如果命中则结束，否则进入查询关键字所属范围的子节点。
2. 重复上述操作，直到所对应的子节点指针为空（或者已经是叶子节点）。

• 其搜索性能等价于在关键字全集内做一次二分查找。

插入

插入操作是指插入一条记录，即“(key,value)”的键值对：

• 如果 B 树中已存在需要插入的关键字（“key”），则用需要插入的 value 替换旧的 value。
• 若 B 树不存在这个关键字（“key”），则一定是在叶子结点中进行插入操作。

插入过程：

1. 若该结点中关键字个数 < 最大值（“m-1”），则直接插入（对应的子节点）。
2. 如该结点中关键字个数 = 最大值（“m-1”），则将引起结点的分裂：
   1. 以中间关键字为界将结点一分为二，产生一个新结点，并把中间关键字插入到父结点中。
   2. 向父亲结点插入中间关键字的时候，重复以上两个步骤。

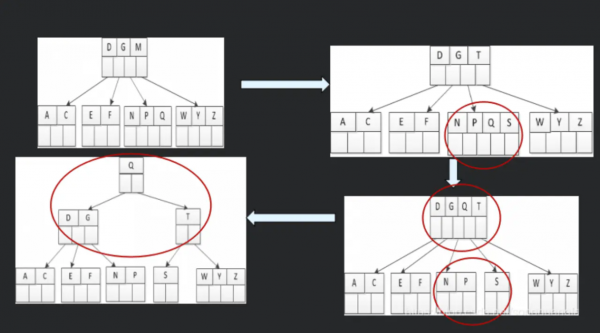
• 最坏情况是一直分裂到根结点，建立一个新的根结点，导致整个 B树 高度增加：
  • 因为插入导致的分裂节点会向上插入，所以不会导致叶子节点的层数不一致。

  

删除

删除操作是指根据关键字（“key”）删除记录对应的节点：

• 如果 B 树中的记录中不存对应关键字（“key”）的记录，则删除失败。

删除过程：

1. 如果当前需要删除的节点位于非叶子结点上，则用后继节点覆盖要删除的节点，然后在后继节点所在的子支中删除该后继节点。【看作删除后继的叶子节点】
   • 此时后继节点一定位于叶子结点上。【后继结点，即中序遍历的后继节点】
2. 如果当前需要删除的节点位于叶子结点上：
   1. 如果删除之后，节点的关键字个数 >= 最小值（“m/2”），直接删除；
   2. 如果删除之后，节点的关键字个数 < 最小值（“m/2”）：
      1. 若此时，兄弟节点的关键字个数 > 最小值（“m/2”）：先将父节点的关键字下移到该节点，然后将兄弟节点的关键字移动到父节点（为了保证子树有序）。
      2. 若此时，兄弟节点的关键字个数 = 于最小值（“m/2”）：先将父节点的“介于该节点与兄弟节点之间的”关键字下移到该节点，并将该节点与兄弟节点的关键字合并，形成一个新的节点；

         然后根据需要再平衡【因为可能：1、新节点关键字个数 > 最大值（“m-1”）；2、父节点关键字个数 < 最小值（“m/2”）】。

      • （有些结点可能即有左兄弟，又有右兄弟，任意选择一个兄弟结点进行操作即可）